近日，数理科学学院张本龚教授带领的应用数学与交叉科学研究中心团队（以下简称“中心”）连续在《chaos》、《Fractals》、《Frontiers in Genetics》、《Journal of Differential Equations 》、《Journal of Graph Theory》等国际顶级期刊上发表多篇最新研究成果论文。

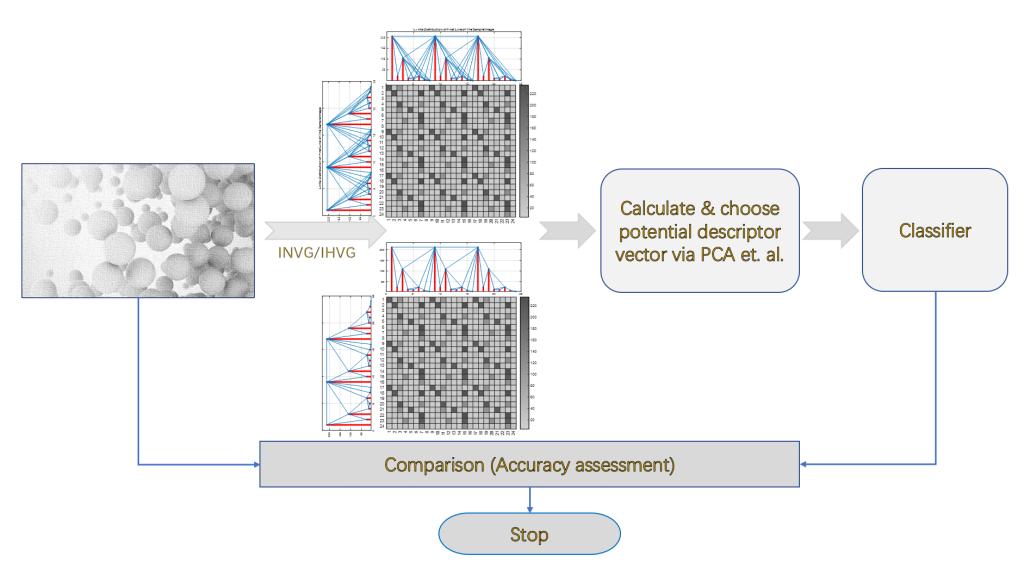
《Chaos》（IF：3.642）上发表了题为：Texture Classification Based on Image (Natural and Horizontal) Visibility Graph Constructing Methods的论文，该论文通讯作者为我校应用数学与交叉科学研究中心刘杰教授，第一作者为研究生裴来凡和李朝辉同学。纹理分类在医学图像分析等领域有着广泛的应用。本文提出了一种基于可视图的纹理分类方法。首先，将数据集中的每个Brodatz纹理图像转换为相应的IVG（图像可视图）和IHVG（图像水平可视图）。然后，提取其度分布P(k)，并将其输入到不同的分类器中。主成分分析（PCA）应用于输入向量，以减少特征数量并避免最终过拟合，并采用5-折交叉验证程序。利用人工纹理图像的IVG二次判别分析法（QDA）可获得100%的分类准确率。在自然纹理图像的IHVG上，利用线性支持向量机可以获得94.80%的分类准确率。文章DOI链接https://doi.org/10.1063/5.0036933。

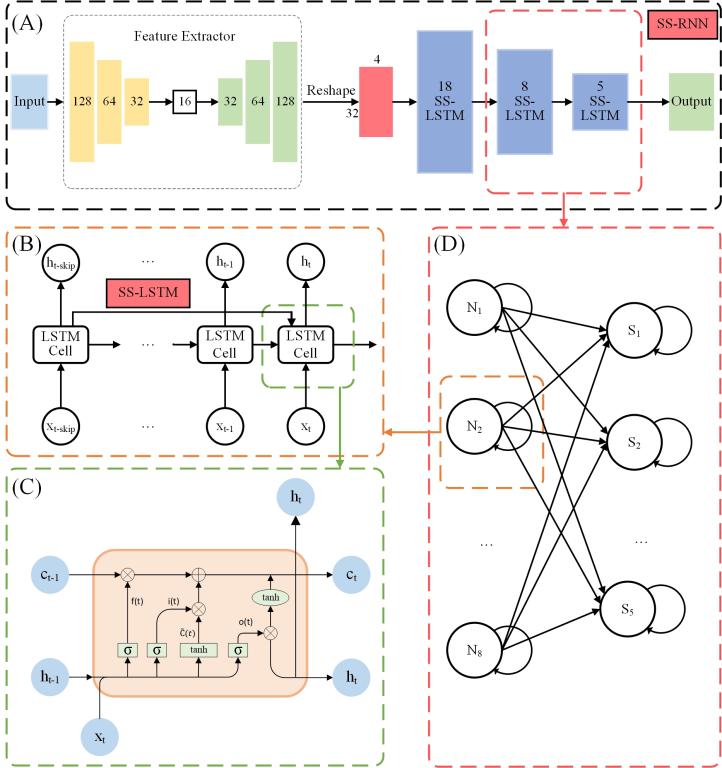
《Frontiers in Genetics》（IF：4.6）在线接收题为：SS-RNN: A strengthened skip algorithm for data classification based on recurrent neural networks的论文，该论文通讯作者为我校应用数学与交叉科学研究中心张本龚教授，第一作者为研究生曹文洁同学。为了有效地捕获序列数据中的长期依赖关系，文章提出SS-RNN模型，它允许历史信息通过不同的方式再次添加至当前时刻。文章共设计了六种不同的跳跃模式，模拟添加过去信息的可能方式，并在五个与疾病相关具有不同大小和数据类型的数据集上进行测试。通过与原始LSTM、GRU、Bi-LSTM以及最新的方法RNN+GRU, RNN+LSTM, MCNN进行比较，结果表明，该方法可以显著提高序列数据分类的准确性。此外，最好的方法是不连续的添加，且不需要加权和函数映射的方式，它能有效地解决梯度消失和梯度爆炸的问题，模型性能与跳跃阶数在不同的数据集间也存在一定的关联性。SS-RNN通过优化LSTM模型为提高序列数据的分类精度提供了一种新的思路，因此，使用者也可以通过添加SS-RNN模块来优化自己的网络模型，其对于疾病的分类诊断和精准治疗具有重要意义。文章doi: 10.3389/fgene.2021.746181。

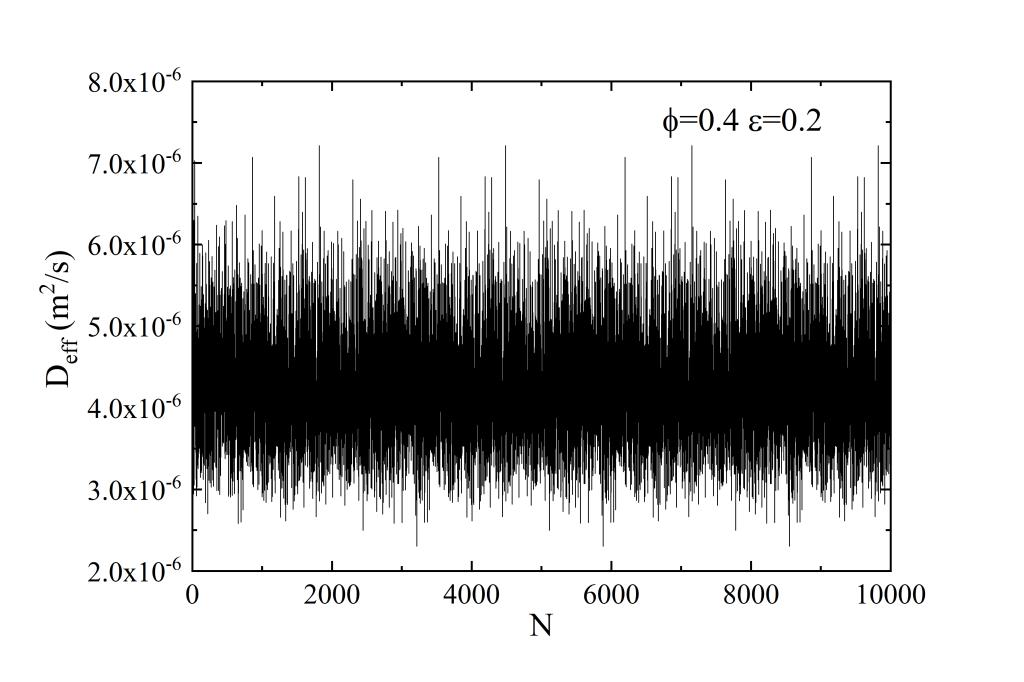
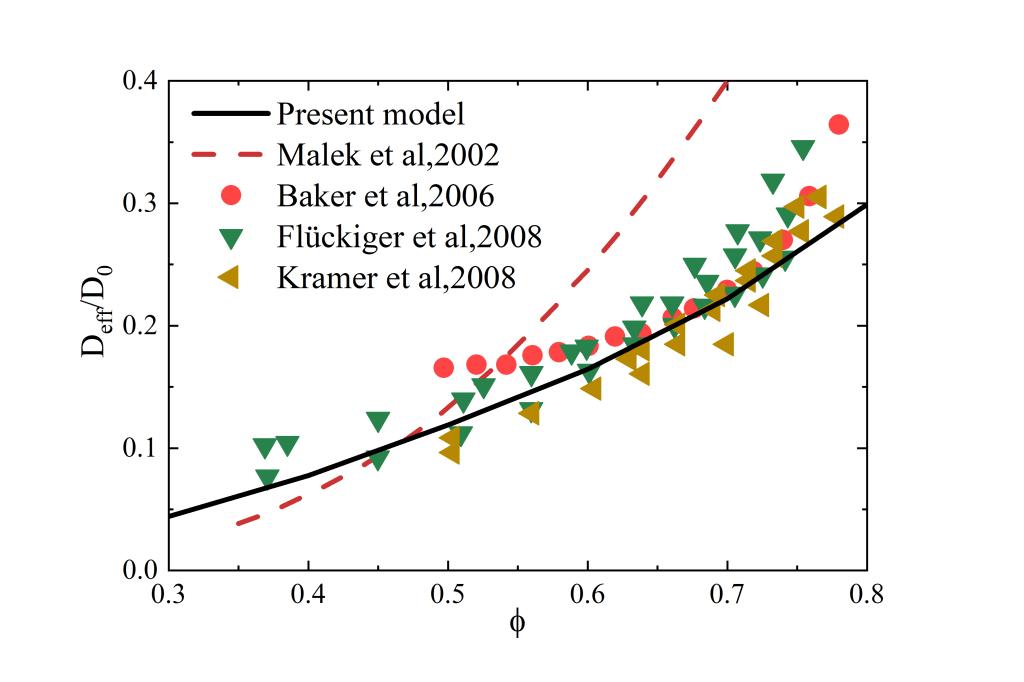
《Fractals》（IF：3.665）在线接收题为：Effective gas diffusion coefficient of fractal porous media with rough surfaces by Monte Carlo simulations的论文，该论文通讯作者为我校应用数学与交叉科学研究中心郑仟副教授，第一作者为研究生尹作壮同学。气体扩散系数是表征多孔介质输运特性的一个重要参数。本文基于微观毛细管的分形特征，采用蒙特卡罗方法研究了毛细管表面粗糙度对气体扩散的影响，提出了粗糙表面多孔介质有效气体扩散系数的概率模型。该模型表示为多孔介质几何参数的函数，如孔隙度、孔隙分形维数、迂曲度分形维数和相对粗糙度。论文着重探讨了相对粗糙度对有效气体扩散系数的影响，结果表明，粗糙表面多孔介质的有效气体扩散系数随着相对粗糙度的增加而减小。此外，该研究还详细分析了多孔介质其它结构参数对气体扩散的影响。该模拟方法可推广用于粗糙表面分形多孔介质中的气体流动和传热过程的分析。

“中心”作为学科建设、科学研究的综合性平台，有力推进了各项事业的发展。作为支撑学科助力“大数据与智慧管理”省级学科群的建设立项工作，“中心”于9月底组织了“新时代数学学科建设与发展研讨会”，广邀国内专家把诊问脉，研讨数学学科面临的挑战、发展的方向、应对的策略，在学界产生了积极影响，提升了“中心”以及学校的知名度。

2021年以来，“中心”团队成员，包括江健博士、朱丽梅博士、陈园博士、阮曙芬博士、王彦波博士、付红波博士等先后发表多篇高水平论文，团队科研能力步入稳定产出阶段。上述发表的三篇最新研究成果，第一作者均为“中心”团队教师所带研究生，标志着“中心”科研反哺教学效果显著，人才培养达到了新水平。

中心简介：为适应国家实施创新驱动发展、服务湖北省实体经济高质量发展、提升我校“双一流”建设水平，在学校的大力支持下，2019年成立应用数学与交叉研究中心。该中心秉承“自由探索、学科交叉、融合发展、服务社会”的发展思路，坚持战略性需求导向，加强基础研究、注重原始创新，优化方向设置布局。通过优化整合资源，加强数学、纺织、计算机等学科间的横向交叉研究，推进学科交叉融合，完善共性基础技术供给体系，实现数学研究从单一学科模式向更包容的多学科交叉合作模式展开。主要围绕科学与工程计算、大数据与人工智能的数学理论方法、复杂系统优化与控制、计算机数学、数学与纺织纤维材料等研究方向。瞄准信息科学、智能与环境、经济与金融安全和生物医学等重大需求中的数学问题。现有全职研究人员20余人，开展了卓有成效的数学、计算机、纺织与材料等基础研究和应用基础研究工作。近年来，获批国家级项目30余项、累计科研进账700余万元、发表高水平论文200余篇，出版学术专著5本，培养研究生20余人。