应用数学与交叉科学研究中心复杂网络团队于2024年3月18日进行每周小组组会，小组全体成员和各位导师共同参加。在这次组会上，由一名研一学生和两名研二学生分别汇报自己的研究进展，然后老师与同学们对汇报内容进行学术探讨，并对存在的问题给出相应的指导和建议。

黄文丽 ：这次汇报了《SIR epidemic model with Mittag-Leffler fractional derivative》。本文讨论了带时滞的Atangana-Baleanu Caputo分数阶导数描述的SIR流行病模型。理论效应和非奇异核构成了Atangana-Baleanu分数阶导数的两个特征，并解释了近年来它在模拟生物现象方面的出现。讨论了所有与分数阶导数阶数密切相关的解的正性；还对解的存在性和唯一性进行了详细的研究。在得到平衡点和再生数后，用Lyapunov直接法讨论了系统的全局稳定性分析。最后提出了同伦摄动法在SIR流行病模型求解中的可能应用。通过在同伦摄动方法中考虑更多的迭代来扩展现有的工作将有助于改进本文。

杨凤鸣 ：本次汇报了一篇文献《Identifying key players in complex networks via network entanglement 》，该研究受量子信息论启发，创新性地提出了复杂网络中节点纠缠的概念，并利用节点纠缠识别复杂 网络中的关键节点。该方法不仅考虑了复杂网络的局部结构和拓扑信息，而且也考虑了网络的全局 信。研究发现，在极小的时间尺度下，节点纠缠趋于0，而在极大时间尺度下，节点纠缠度可以反 映网络的连通性。在中观尺度上，节点纠缠度同样发挥着重要的作用，可以衡量节点对系统传输性 质的影响。节点纠缠使人们对复杂系统内在的拓扑属性有了新的认识。应用层面，最优网络拆解仍然是一个开放的问题，本文提出的节点纠缠则提供了一种用于网络拆解的新框架；此外，节点纠缠还可以应用于自闭症谱系障碍的诊断支撑，基于节点纠缠的枢纽中断指数在自闭症患者和典型对照组之间存在显著差异，为自闭症诊断提供了有力的工具。节点纠缠作为一种多尺度的网络分析工具，其应用不限于上述领域。在未来的研究中，节点纠缠可能会在更多领域展现其价值，如社交网络分析、生态系统管理、经济网络优化等。节点纠缠方法将量子信息理论的概念应用于复杂网络分析，推进了网络科学与量子物理的交叉融合，不仅推动了理论研究的深入，也为实际问题的解决提供了新的视角和策略。

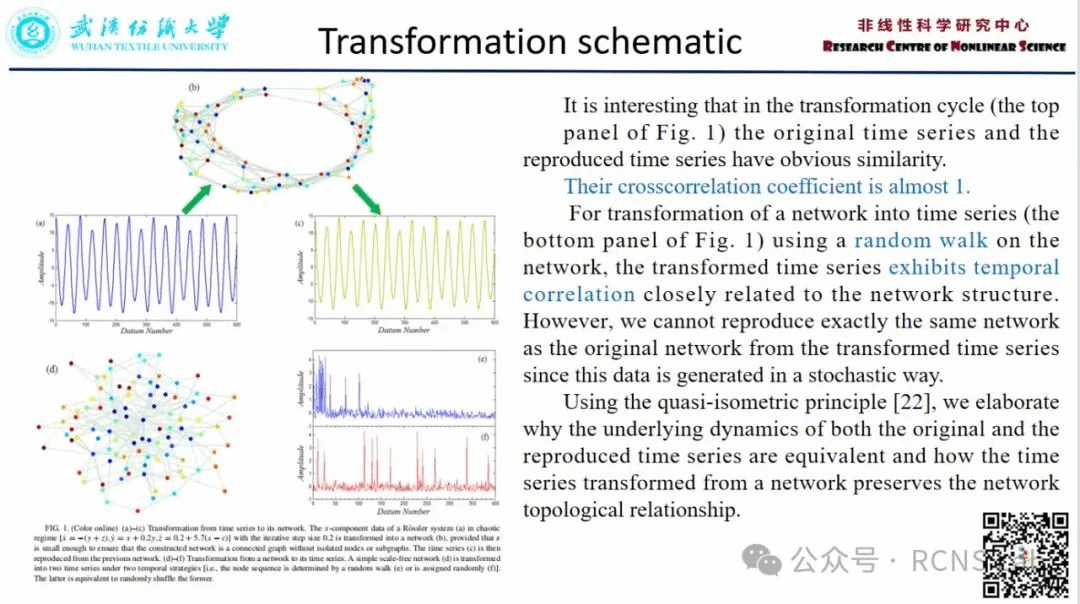
牛浩瀛：本次汇报了一篇文献《Geometrical invariability of transformation between a time series and a complex network 》，基于粗几何理论，我们给出了时间序列和复杂网络之间的动态等价变换。根据拟等距同构映射，我们描述了复杂系统的基本几何特征。分形维数对于时间序列（或复杂网络）及其变换后的对应物是相同的。来自罗斯勒系统、分数布朗运动、合成网络和真实网络的结果支持了我们的发现。本文为时间序列与网络之间的等价变换提供了理论证据。

----------学生汇报照片----------