应用数学与交叉科学研究中心数学与纤维材料团队在2024年3月12日上午9：00于崇真楼3028教室进行每周小组组会，小组全体成员和各位导师共同参加。在这次组会上，由研二研一五名学生分别汇报自己的研究进展，然后老师与同学们对汇报内容进行学术探讨，并对存在的问题给出相应的指导和建议。

徐静蕾：本次组会介绍了一个描述表面扩散对页岩气输运影响的模型。该模型模拟了干酪根孔隙中的多种流动机制，考虑了表面扩散、其对滑移速度的影响以及粘性流和克努森扩散贡献的非线性组合。此外，考虑到表面扩散产生的额外粘性通量，开发了改进的气体滑移模型。使用真实的干酪根特性进行敏感性分析，以确定表面扩散对气体渗透率的贡献。

万荃：本次组会汇报一篇名为《EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks》的文献。EfficientNet文献中，对模型缩放进行了系统研究，发现仔细平衡网络深度、宽度和分辨率可以带来更好的性能。基于这一观点，作者提出了一种新的缩放方法，利用简单而高效的复合系数统一缩放深度/宽度/分辨率的所有维度。并且展示了这种方法在扩展 MobileNets 和 ResNet 时的有效性。

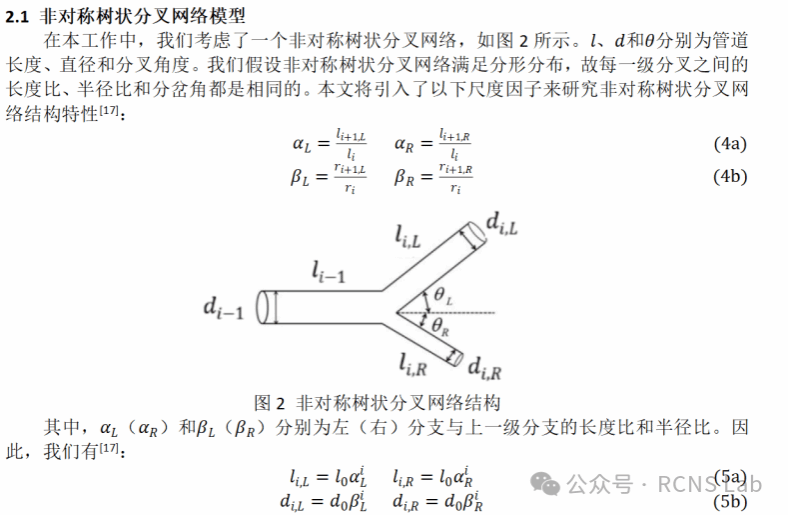
谢磊：本次组会汇报近期工作，针对非对称树状分叉网络的分形结构，采用了两种不同的等效方法计算网络的有效渗透率。第一种通过计算每一级的等效流阻，根据Hagen-Poisille定律计算每一级的流量，按照质量守恒构建等式进行等效，第二种通过计算每一级的等效横截面积和等效渗透率，将每一级等效成一根单管，同样根据质量守恒构建等式，再将整体等效成一根单管计算网络的有效渗透率。

胡佳青：本次组会汇报了液体通过纤维多孔介质的动力学：实验、分析和数值研究。在本研究中，开发了一个稳健的分析和数值模型来预测液体通过纸基板流动。并且综合了多种效应，如纤维的膨胀和粗糙度的影响，液体的蒸发和动态的接触角。所建立的模型对于预测液体通过纸基板的流动具有较强的通用性和现实性。为验证模型的正确性，进行了液体在纸基板上的流动实验。数值模型和解析模型与实验结果吻合较好，最大误差为5%。在未来，该模型可以扩展到不同的液体、纸张类型和环境条件。所建立的模型可用于纸基微流控器件的优化设计。

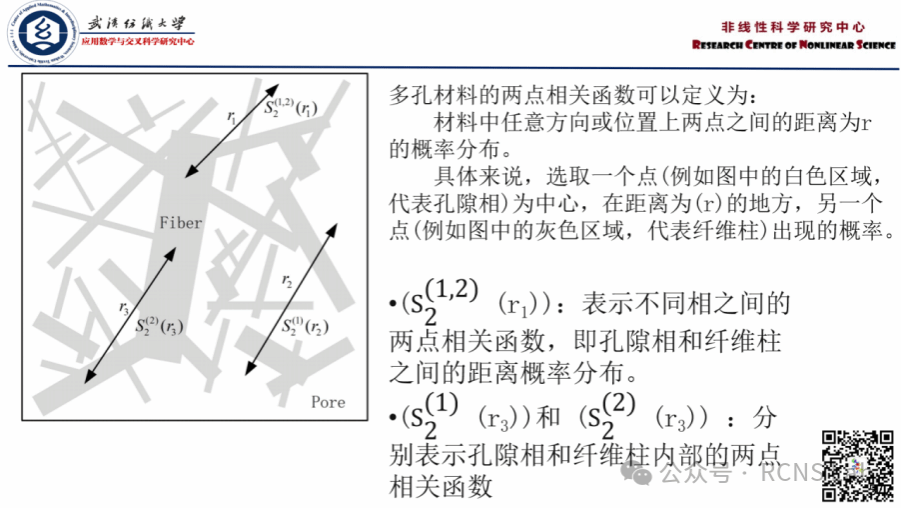
吴仔航：本次组会汇报了一篇名为《Reconstruction of random fibrous porous material and numerical study on its transport properties by fractal Monte Carlo method》的文献。这篇文章开发了一种新的FMCM来数值重建纤维多孔材料的随机和复杂微观结构，并通过有限元法研究了单相流体通过重建的二维随机结构的流动。并相应地考察了微观结构参数对纤维多孔材料有效渗透率的影响。

1.重构纤维多孔材料不同相之间的两点相关函数表明，微观结构的统计信息与孔隙率和分形维数无关。因此，所提出的FMCM为纤维多孔材料提供了一种有效而快速的数值重建方法。

2.二维纤维多孔材料中流体流动的数值计算结果与现有的经验公式吻合良好，也证明了本文重构方法和单相流体流动数学模型的有效性。

3.孔隙率和分形维数都对纤维多孔材料的有效渗透性有显著影响。增加孔隙度和降低分形维数将提高有效渗透率。与纤维柱长度相比，纤维柱宽度的分形维数的影响更为明显。